| ◆ 二重積分 | ||||
| 次の積分の式は, | ||||
| |
||||
| 「微小面積dAに,yをかけて,面積A全体にわたって積分する」と定義されている。 | ||||
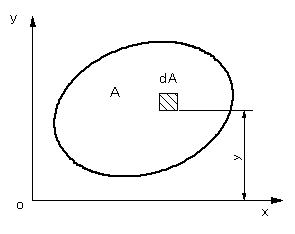 図 16 閉曲線で表される面積Aの図形 |
||||
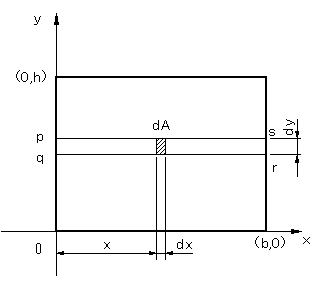
| この式は,薄い板の重心の位置を求めるときに物理学などで使う式である。 図の閉曲線の式が与えられれば,具体的に積分の値を求めることができる。次に,この積分を用いて,すでに解っている長方形の面積を計算する。 図 17(a)のように,高さh,幅bの長方形内の微小面積dA(=dxdy)をとる。xとyの変域は |
||||
| である。 | ||||
|
||||
| 図 17 厚さtの長方形の板が水平におかれている場合の重心の位置 | ||||
まず,微小面積dAの高さdyは一定として,長方形pqrsの面積をxについての積分によって計算すると |
||||
| |
||||
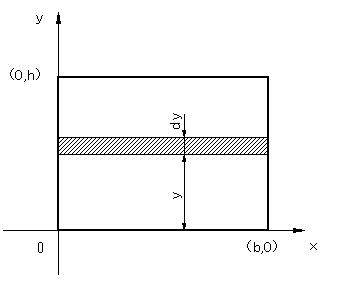
| となる。つぎに,(b)のように微小面積pqrsをyについて,0からhまで積分する。 | ||||
| |
||||
| となる。こうすることによって長方形の面積全体にわたってx,yを変化させ,微小部分の和を求めたこと,つまり,積分したことになる。 この計算過程を連続して書くと次のようになる。 |
||||
| |
||||
| このように,境界における xと,yの関係,変域がわかると普通の積分と変わりなく計算できる。二回積分が入るので二重積分,あるいは,もっと積分記号が重なってはいる重積分という。 物理学では,重心の座標は |
||||
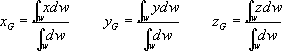 (38) (38) |
||||
| の式で与えられる。 |
||||
| 平行力の合成のページで述べているように、重心の位置は、物体の各部分に作用する重力(鉛直、下向き、平行力)の合力が作用する位置である。この合力の大きさは物体の全重量W(=Mg)に相当する。ここでは、重心の位置を求める過程で上式が三重積分になることを解説する。 |
||||
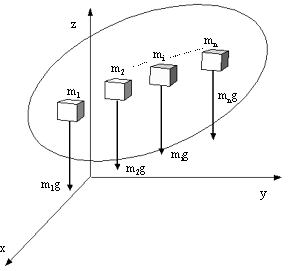 図18 |
||||
| 物体(質量M)をn個の微小部分にわけ、それぞれの質量m1, m2, ・・・ mi ・・・・ mn とし、これらの位置をそれぞれ、(x1,y1,z1),(x2,y2,z2),・・・(xi,yi,zi),・・・(xn,yn,zn)とする。微小部分に作用する重力は m1g, m2g, ・・・ mig ・・・・ mngである。これらは鉛直下方に作用する平行力であるので合成することができる。これらの合力の大きさは |
||||
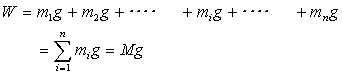 (39) (39) |
||||
| となる。 一方、合力の作用点は、もう一つの釣り合いの条件、モーメントが等しいことから求めることができる。物体は3次元であるので、作用点は図18のようにx,y,z座標で表す必要がある。x座標に関する微小部分に作用するモーメントの和をTx 、y,z軸に関してもモーメントの和をTy、Tzと置くと |
||||
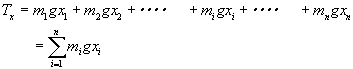 (40) (40)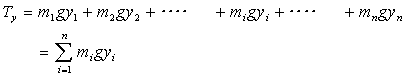 (41) (41)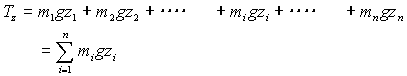 (42) (42) |
||||
| と求められる。 物体に働く重力の合計は、重量Wである。 |
||||
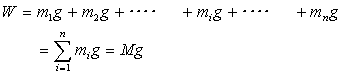 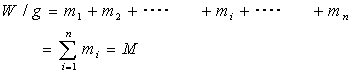 (43) (43) |
||||
| 別ページ「力学の基礎-平行力の合成」で述べているように、平行な重力の合成を行う。合力の作用点(xG,yG,zG)と置く。合力の大きさは、W=Mgである。 |
||||
| x軸に関するモーメントが等しい Mg・xG =Tx y軸に関するモーメントが等しい Mg・yG =Ty Z軸に関するモーメントが等しい Mg・zG =Tz |
||||
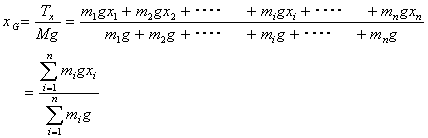 (44) (44)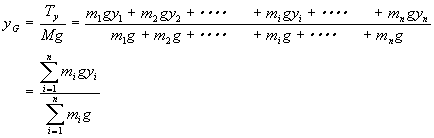 (45) (45)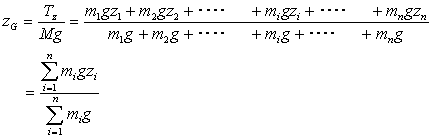 (46) (46) |
||||
| 別ページ「微分法と積分法」の式(16)を求めたのと同じ考え、微小部分mi を限りなく小さく、すなわち、n→∞にすると積分することに相当するので |
||||
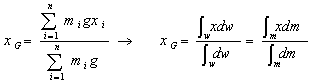 (47) (47)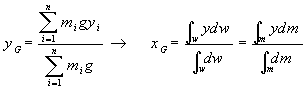 (48) (48)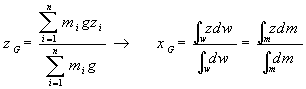 (49) (49) |
||||
| と書ける。 さらに、均質な物体の場合、体積V,密度ρ,重力加速度gとすると,w=mg=ρgVであり,重力の大きさは体積に比例する。 dw=ρgdV 、dm=ρdV |
||||
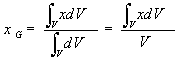 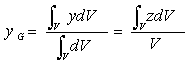 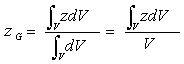 (50) (50) |
||||
| さらに、微小部分の大きさを図19のように置くと、dV=dxdydz、 M=ρVとなるので |
||||
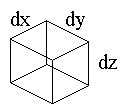 図19 微小部分の寸法 |
||||
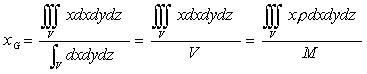 (51) (51)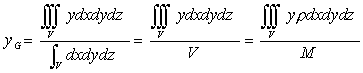 (52) (52)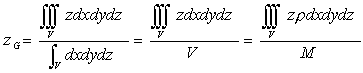 (53) (53) |
||||
| 重心の位置を求める式は三重積分となる。物体の形状をx,y,zで表し、x,y,zの変域が分かれば積分を行って求めることができる。実用的な物体の形状としては複雑ではないので、二重積分で示したように簡単な積分に直すことができる。 均質で厚さtの一様な板が水平におかれた場合は,重力は面積Sに比例に比例する(V=tS,w=ρgtS)から次のようにかける。この場合,厚さ一定であるから、2次元で考えることができる。 dV=tds=tdxdy |
||||
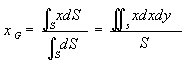 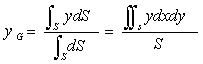 (54) (54) |
||||
| この場合は複雑な形状の場合は別として、二重積分の項で述べた方法に帰着する。式(54)は、ydxdyがy2dxdyになった、断面二次モーメントを求める場合の具体的な断面形状の計算例は「はじめての材料力学」(小山信次、鈴木幸三著、森北出版)で述べている(p.95~99)。 |
||||
| ■数学公式集 一般の教科書に出ていない関数の不定積分などほとんどの関数の不定積分が掲載されています。 「岩波 数学公式Ⅰ 微分積分・平面曲線 」、森口, 一松, 宇田川 著 、岩波書店 材料力学、弾性論以外の専門には 「岩波 数学公式Ⅱ 級数・フーリエ解析」、森口, 一松, 宇田川 著、岩波書店 「岩波 数学公式Ⅲ 特殊函数 」、森口, 一松, 宇田川 著 、岩波書店 |