| 極値統計について | |||||
| 小 山 信 次 | |||||
| はじめに | |||||
| 最近、極値統計の検索からホームページを訪問してくださる方が多く、報告書では省略したためにわかりにくい部分がありますので、具体的に、極値統計法について書いてみました。1995年に、石油タンクの寿命推定に極値統計を適用しました。当時は、「装置材料の寿命予測入門―極値統計の腐食への適用」 、腐食防食協会で勉強しました。腐食例が多いなど極値統計については詳細に書かれている著書ですが、残念ながら現在は絶版になっているようです。 |
|||||
| 1. | 極値統計を理解するための基本的な知識について | ||||
| 1.1 | 度数分布表とヒストグラム | ||||
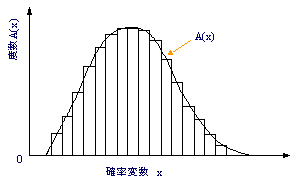
| 腐食の場合を例に取ると、サンプリングした腐食データを腐食量を範囲に分け、範囲に入る度数を調べ、度数分布表に表す。表1では0.1mm間隔に分け、度数Aを調べている。この場合、減肉量(mm)が確率変数xになり、確率密度fは、各度数Aをサンプリング データ総数Nに1を加えた値で割った値、A/(N+1)になる。これを平均ランク法と言う。表1の場合は サンプリング データ総数N=100である。 |
|||||
| 表1 度数分布表 | |||||
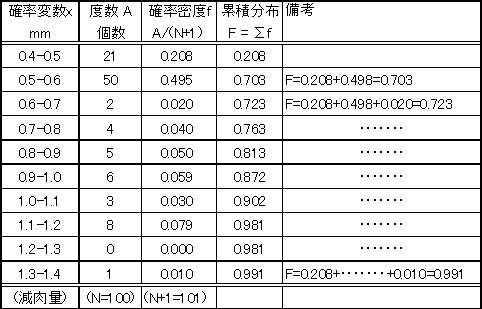 |
|||||
| ヒストグラムは 確率変数xと度数Aの関係を棒グラフに表したものである。 | |||||
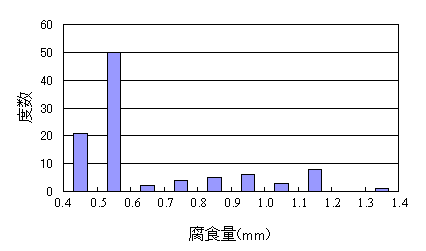 図1 腐食データのヒストグラム 最大値は1.3-1.4mmの範囲に |
|||||
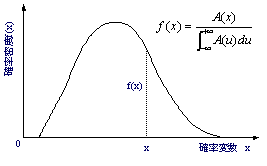
| 1.2 | 密度関数f(x) | ||||
| 度数を確率変数xの関数としてA(x)と定義すると 確率密度関数f(x)は次の関係にある。関連する事項について次式に示す。Nはサンプリング データ総数 | |||||
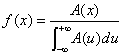 |
|||||
|
|||||
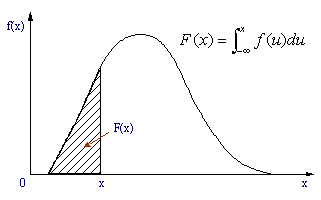
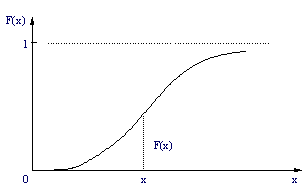
| 1.3 | 累積分布関数 F(x) | ||||
| 表1の累積分布を関数F(x)とする。確率密度関数f(x)との関係は次式のようになる。 |
|||||
| |
|||||
|
|||||
| 2. | 極値統計の理論とその方法 | ||||
|
●均一腐食 → 平均値問題 ●孔食・すきま腐食・応力腐食割れ等の局部腐食 → 極値問題
多数の局部腐食のうち、最も深く進行し、材料の肉厚を貫通するまでの時間がその材料の寿命。石油タンク底板の寿命を考える場合に、局部腐食の深さに関して、その最大値が問題となる。
|
|||||
| 2.1 | 腐食現象の極値分布について | ||||
| ある石油タンクの底板の裏面腐食の最大値を推定する。一定面積をもつ領域をn箇所選び、それぞれの領域から得られるデータからタンク底板全面積における最大腐食量を推定 |
|||||
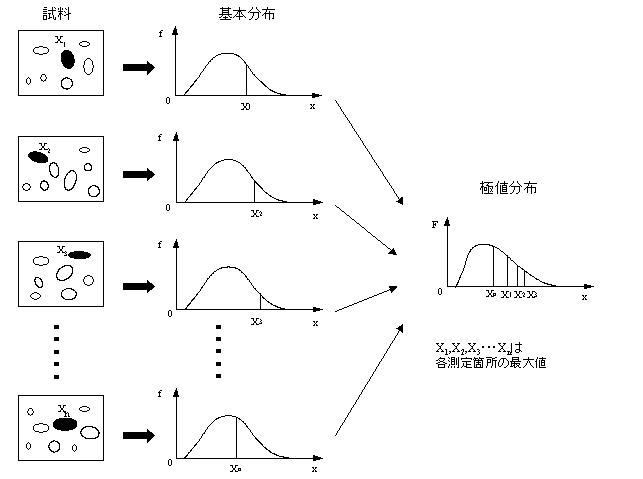 |
|||||
| 図6 最大値の度数分布 |
|||||
|
n箇所の測定値の最大値をそれぞれ、X1, X2, ・・・・・・・Xi ・・・Xn とする。最大値 X1, X2, ・・・・・・・Xi ・・・Xn の分布が極値分布である。表2にn=23の場合の最大値の度数分布表を示した。
最大値の度数分布から以下の値を計算する。
(1).累積度数Fiの計算
最大値の分布を検討する場合、度数(fi) を小さい方から累積し、Fi を計算する。
(2).累積分布Fi/(n+1)の計算と二重指数確率紙へのプロット
累積度数(Fi)を試料個数nに1を加えた値(n+1)で割って累積分布(Fi/(n+1))を算出する(表1のFの計算を参照のこと)。nはデータ数である。平均ランク法という。結果を表.2に示した。これを二重指数確率紙に、x軸上に腐食量を目盛り、各クラスの上限値をx値とし、Fi/(n+1)をFI(x)値としてプロットする。表2の場合、n=23である。1カ所当たりのサンプリングデータ数は100である。
|
|||||
表2 最大値の度数分布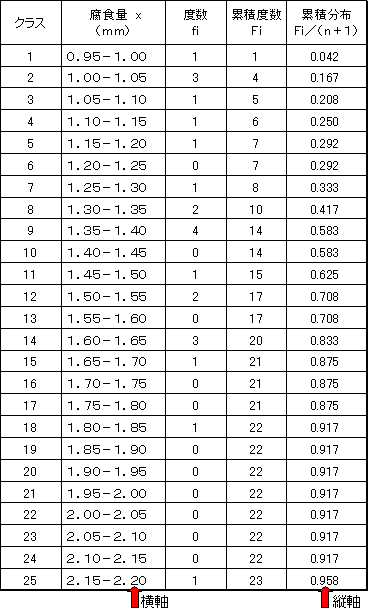 |
|||||
| 2.2 | 二重指数分布の適用の判断 | ||||
|
二重指数分布は、Gumbel分布とも呼ばれている。これには,最大値分布と最小値分布がある。局部腐食による損傷おいて一番問題となるのは、その最大侵食量、それによる装置の最小寿命の予測であることに対応している。
最大値分布FI(x)、最小値分布F−I(x)の式は次式によって与えられる。
FI(x)=exp[−exp{−(x−λ)/α}] -∞<x<∞
F−I(x)=1−exp[−exp{−(x−λ)/α}] -∞<x<∞
λ:位置パラメータ[=最頻値] α:尺度パラメータ
それぞれの密度関数は、
fI(x)= (1/α)・exp[−(α−λ)/α−exp{−(x−λ)/α}]
f−I(x)=(1/α)・exp[(α−λ)/α −exp{(x−λ)/α}]
で与えられる。
ここで,α、λは位置パラメータ,尺度パラメータと呼ばれ,α>0である。密度関数が導かれる過程において、xが大きい領域で基本分布が指数分布となることが仮定されている。極値解析を行う場合、基本分布が不明であっても手続き上不都合はないのであらかじめチェックする必要はない。ただし、最大値のデータが推定された二重指数分布に適合しているかどうかは検定によって確かめることになる。
|
|||||
| 2.3 | 二重指数確率紙を利用したタンク底板の寿命推定 | ||||
| 最大値分布FI(x)の両辺の自然対数を2回とる FI(x)=exp[−exp{−(x−λ)/α}]
λ :位置パラメータ[=最頻値]、α :尺度パラメータ
ここで,
FI(x)= exp(-e-y) -∞<x<∞
F−I(x)=1−exp (-e-y) -∞<x<∞
|
|||||
|
●二重指数確率紙
二重指数確率紙は、直交座標系の1軸に
を目盛り,他の一軸に確率変数xを目盛った方眼紙である。縦軸にFI(x)、横軸にxにとり、データをプロットして,直線のまわりのばらつきが一定の範囲内にあれば二重指数分布に従っていると判断される。この直線からパラメータα、λを求める。y と x が y = ax + b の直線となることがプロットして明確になれば最小二乗法で計算することができる。
となるので、y = 0 、F1(x) = 0.368 を与えるx の値がλとなる。
|
|||||
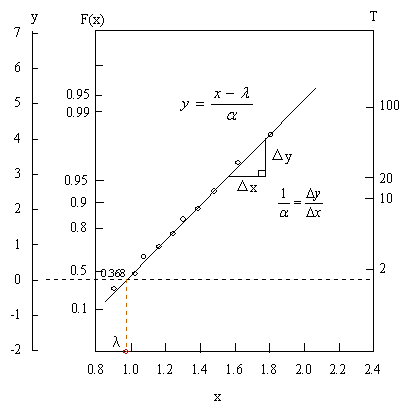 図7 二重指数確率紙 プロットデータは説明用 |
|||||
| 一方、直線の傾きから | |||||
| のようにαを求めることができる。 |
|||||
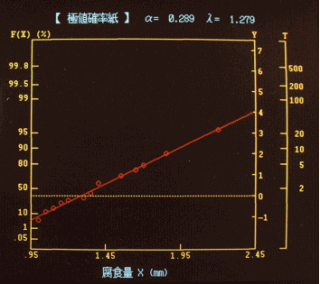 図8 コンピュータ処理した場合の確率紙でのデータ
直線は最小二乗法により決定している。α、λの値も自動的に計算
|
|||||
|
表2のデータの パラメータλ,αを求めた結果、y=3.4573x−4.426が求められたので、データ例の場合は、α=0.289、λ=1.253が得られた。分布関数FI(x)は、データ例の場合は、
FI(x)= exp[-exp{-(x-1.253)/0.289}]
となる。
|
|||||
| 2.4 | 寿命予測の方法 | ||||
| 1つのサンプル領域から,1個の最大値uが得られる場合に、ある値aより大きな値が得られるまでには何カ所の領域について調べることになるのかを考えてみる。今,この数をNとすると、その確率はP(N)は次のようになる。はじめから(N−1)箇所までのuのそれぞれがaより小さい確率がF(a)であるから、(N−1)箇所すべてにおいて、aより小さい確率はF(a)N−1である。N番目の領域で、uがaより大である確率は{1−F(a)}である。従って、
P(N) ={F(a)}N−1・{1−F(a)}
Nの期待値Tは再帰期間である。
F<1であるから
T=1/{1−F(a)} (5)
となり、確率紙におけるT目盛りとF(x)目盛りの関係は(1)式の関係がある。
次にTを設定する。今考えている全底板を対象領域に考えると、次式が成り立ち、データを適用すると次式の結果となる。 【例1】
T=(全低板面積)/( サンプル領域1つの面積)
= (π/4)・D2/(10×10) = 5,772,300 ただし,タンク直径D=27.11m、測定領域は10 mm×10 mmである。
Tに対応するx(xmaxとおく)を求めると、
−l n{−l nFI(x)}=(x−λ)/αとT=1/{1−F(a)}式から
xmax=λ+α・l n{−l n(1−1/T)}
となり,T>>1であるから,
xmax=λ+α・l n T
T=577230,λ=1.253, α=0.289を上式に代入すると、xmax=5.473が得られる。
残存寿命をZ[年]とすると、
Z=(残存板厚)/(腐食速度) =(to−t)/Y = 0.0025 年
ここに、初期板厚to=6.0 mm、現状の最小板厚(xmax)、t= 5.473、タンクの使用年数Y=15年である。
|
|||||
表3 タンク仕様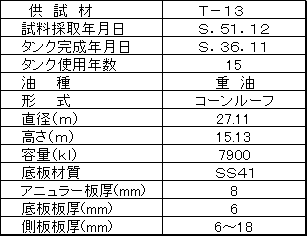 |
|||||
|
【例2】 サンプリング領域の500倍の面積を有する試験片に生ずる最大孔食深さを推定する
500倍の面積を有する試験片は試験片数N=500の小面積試験片をサンプリングした場合と同一であり、材質も同じであれば確率紙で同一直線上に乗る。F=N/(N+1)=500/501の再帰期間Tを計算すると T=1/(1-F)=N+1=501, 501≒500 , T ≒N
点Aを通る横軸と縦軸に平行な直線を引くとB点のxの値が求める500倍の面積を有する試験片に生ずる最大孔食深さと推定できる。
*【例1】では数式からxmaxを求めたが、【例2】では確率紙から図式的にxmax を求めた。
|
|||||
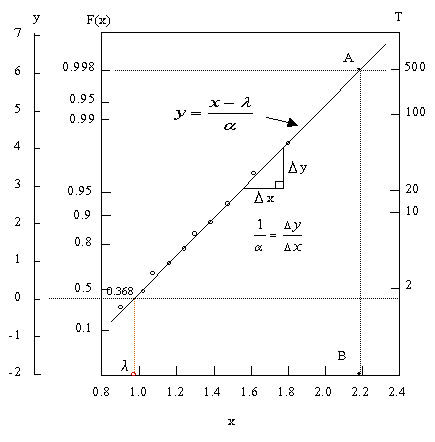 図9 |
|||||
| 2.5 | 推定された確率分布の妥当性の検討 | ||||
| これまでに述べたような方法で、推定された二重指数確率分布が実測値を表しているものであるか否かを判定する必要がある。χ2検定とK.S検定法がある。ここでは、χ2検定を得られた結果に対して適用する。
観測されたデータをk個のクラスに分けてi番目のクラスの下限をβi,上限をβi+1、また、このクラスにデータの数をNiとし、全データ数をNとする。このとき、i番目に含まれるデータの期待度数は次式で与えられる。 このとき
は、自由度 k-C-1 のχ2分布に従うことが知られている。Cは未知の分布のパラメータの数である。測定されたデータを使って当てはめようとする分布のパラメータを推定した場合、パラメータは未知であるとして扱われる。χ2検定は求めた値χ2がχ2分布表から求めた値より小さければ分布に適合すると考える。
χ2分布表から求める値は、今ある定数αを考えて を満たすαである。ここに、hk-1(x) は
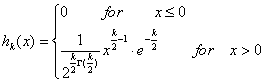 であり、Γ(x)はΓ関数である。
f(x)に、ある値aをとり、上式に代入すると、 |
|||||
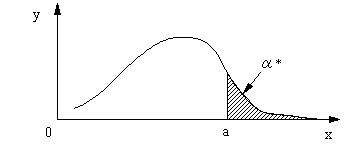 図10 |
|||||
|
α*はχ2値すなわち、xがaよりも大きい確率を与える。このα*が十分小さく、(a≦x)とすると、そのようなx値が発生することはまれであり、Niは実測値であるからxがaより大きくなってしまったのは、N・Pi すなわち推定した理論値に問題があったわけである。すなわち、理論式が適切ではないと判定される。この判定内容はα*の値によって左右される。α*は危険率あるいは有意水準と呼ばれる。
【計算例】
石油タンク底板腐食量のサンプリングデータを表4のようにクラス分けし、腐食量の範囲に存在する実測値から、推定された二重指数分布が実測値を表しているかどうか判断するために、このデータの場合のχ2検定を行う。
i番目のクラスに含まれるデータの期待度数は次式で与えられる。
具体的に、Table.3で、i=2のとき、β1 = 1.25、β2 = 1.55 である。
F(x)と f(x)の関係、
から
FI(x) = exp[−exp{−(x−1.253)/0.289}] λ=1.253, α=0.289
データの期待度数は
N・Pi = N{F(β2 )-F(β1 ) N=23
となる。
同様に各クラスのχ2値は (Ni - N・Pi )2/N・Pi で計算される。計算結果を表4に示した。
|
|||||
表4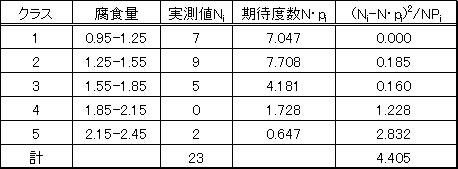 |
|||||
|
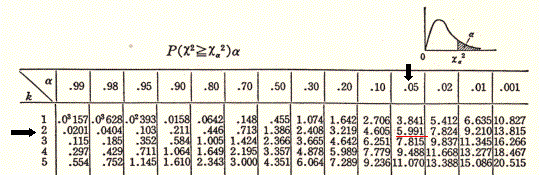
ここで,上記の方法で推定された二重指数分布が実測値を表しているかどうか判断するために、このデータの場合のχ2検定を行う。計算の結果、χ2値は4.405となった。ここで、χ2 分布表を参照することになるが、自由度kは、k=(クラス数−パラメータ数−1)である。クラス数5,分布のパラメータ数はαとλの2つ。k=5-2-1 =2となる。有意水準*を5%とすると、
χ=4.405,a=5.991
となり、χ<aである。従って二重指数分布(3)式は5%の危険率で棄却されない、すなわち二重指数分布の仮定は正しいと言うことができる。
|
|||||
表5 χ2 分布表
 |
|||||
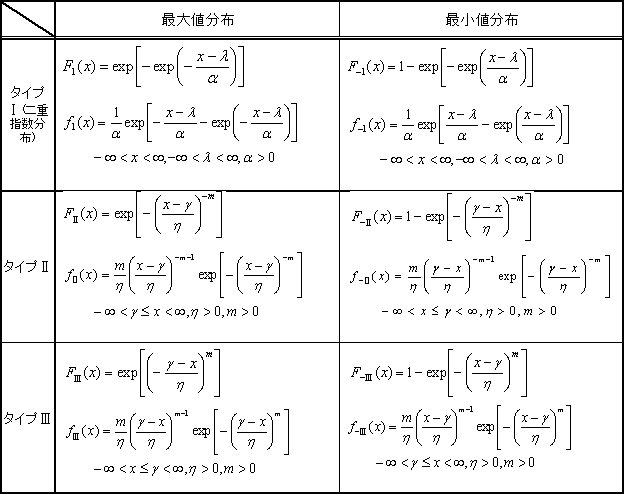
| 3 | 極値分布の種類等 | ||||
表6 極値分布の種類1)
 |
|||||
表7 腐食データの基本分布1)
 |
|||||
表8 腐食データの統計処理に使用する分布1)
 |
|||||
|
参考文献
1) 装置材料の寿命予測入門―極値統計の腐食への適用 、腐食防食協会
*この書籍は具体例が豊富で極値統計について最も詳細に書かれている。残念ながら現在は絶版になってしまっている。 |
|||||
| ● | 十千万(トチマン)、二重指数確率紙(極値確率) http://www.tochiman.co.jp/index_pd_1.html |